Posted by Andreas Klintberg

Truth Discovery in Practice — Aggregating Conflicting Datasources

If one source says Microsoft’s headquarter is in Seattle, and another source has it in San Francisco, how do we determine which one is more plausible? The literature calls this the truth discovery or veracity problem.

In this blog post Andreas Klintberg from our Knowledge Graph team shares how Fairhair.ai uses the Truthfinder algorithm to fuse thousands of data points from dozens of sources for our knowledge graph.

The Veracity Problem (Truth Discovery)

The vision of Fairhair.ai is to harness the power of diverse online sources by using 5 advanced AI systems in combination to surface, structure, connect, understand, reason and derive actionable insights. In the Fairhair.ai Knowledge graph team we are connecting, cleaning and distilling all this information from different sources into one coherent store and view.

All these data points tells us something different about each entity, sometimes complementary and sometimes conflicting. Online sources vary in both coherence, reliability and accuracy.

Our customers wants to answer questions such as “Which of Pepsi Co competitors in the beverage segment has done the most acquisitions?” 

To answer this question we need to aggregate all information pertaining to Pepsi Co and its competitors. This information is available in both unstructured format such Wikipedia, news articles, corporate websites; and structured sources i.e DBPedia and Wikidata. How do we fuse information from all these sources to create one source of knowledge? [5].

This problem is often called the veracity problem or truth discovery: which information, from a range of conflicting sources, is the most accurate information [1].

In this post I’ll walk you through one possible approach to this problem for structured data integration and provide coding examples and explanations. 

TruthFinder

TruthFinder [1] is an algorithm that tries to solve the veracity problem in an iterative process, similar to the HITS algorithm or PageRank. However in comparison to the HITS algorithm, which tells you the odds of a random walker/surfer ending up on the source, TruthFinder emphasizes correctness of facts and not the quantity of facts provided from that source[1, 7].

We’ll start out with a real world dataset [2] of 1265 books and 26554 author attributes from 895 different e-commerce sites. It can be downloaded directly from here.

Representing the Problem

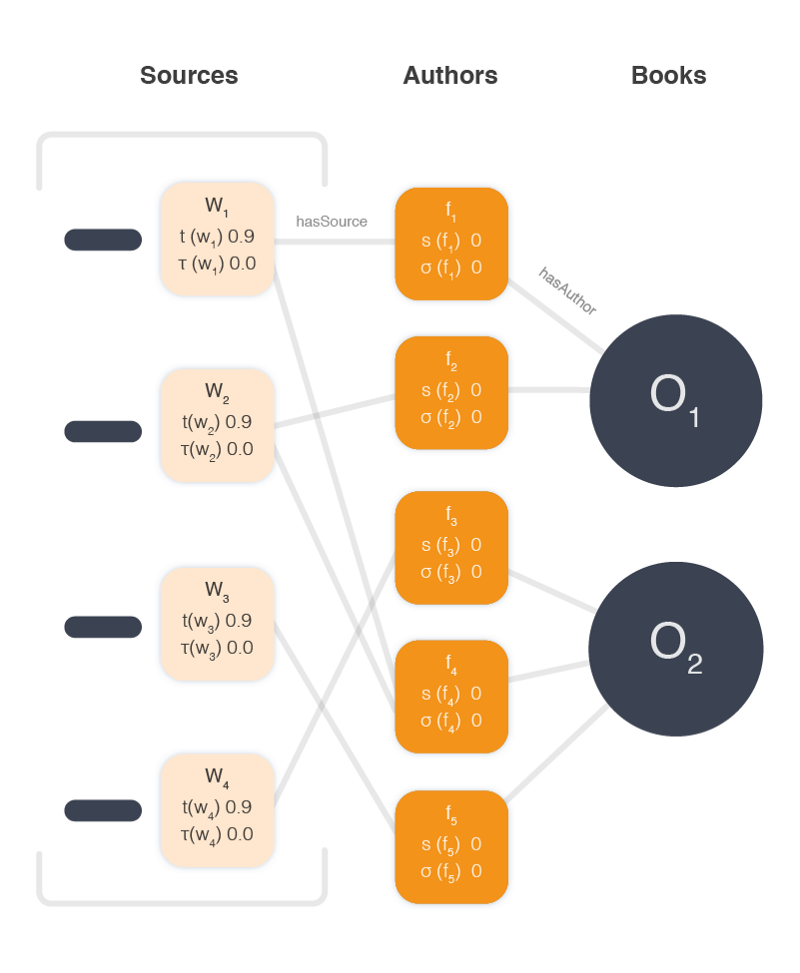
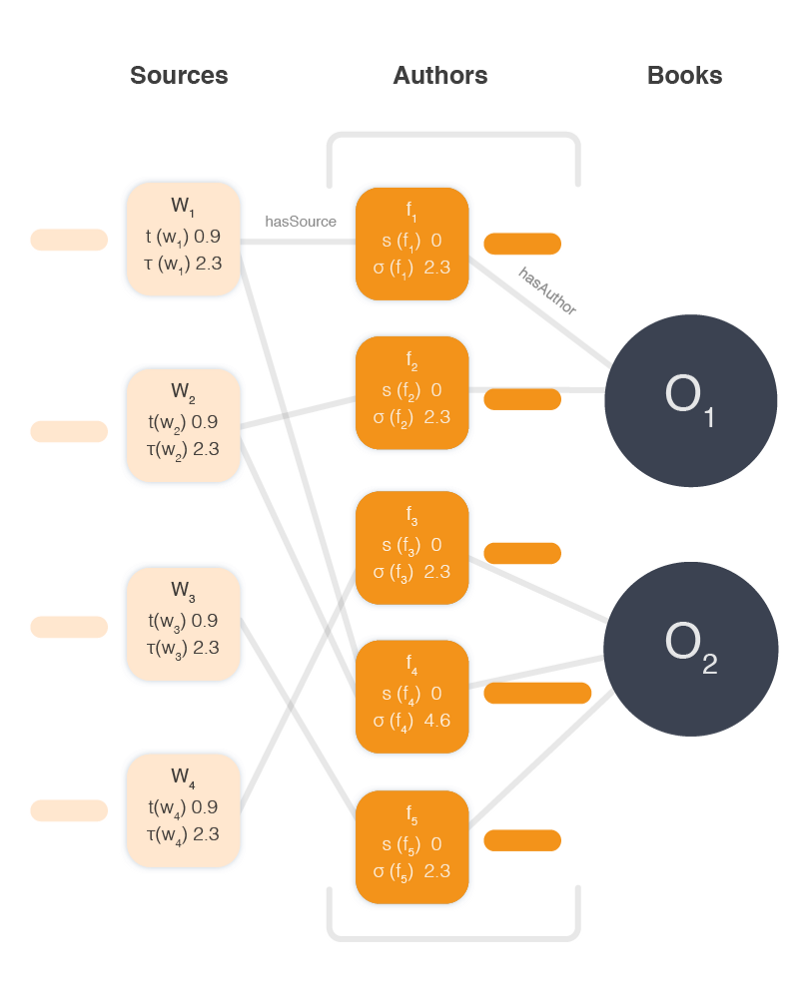
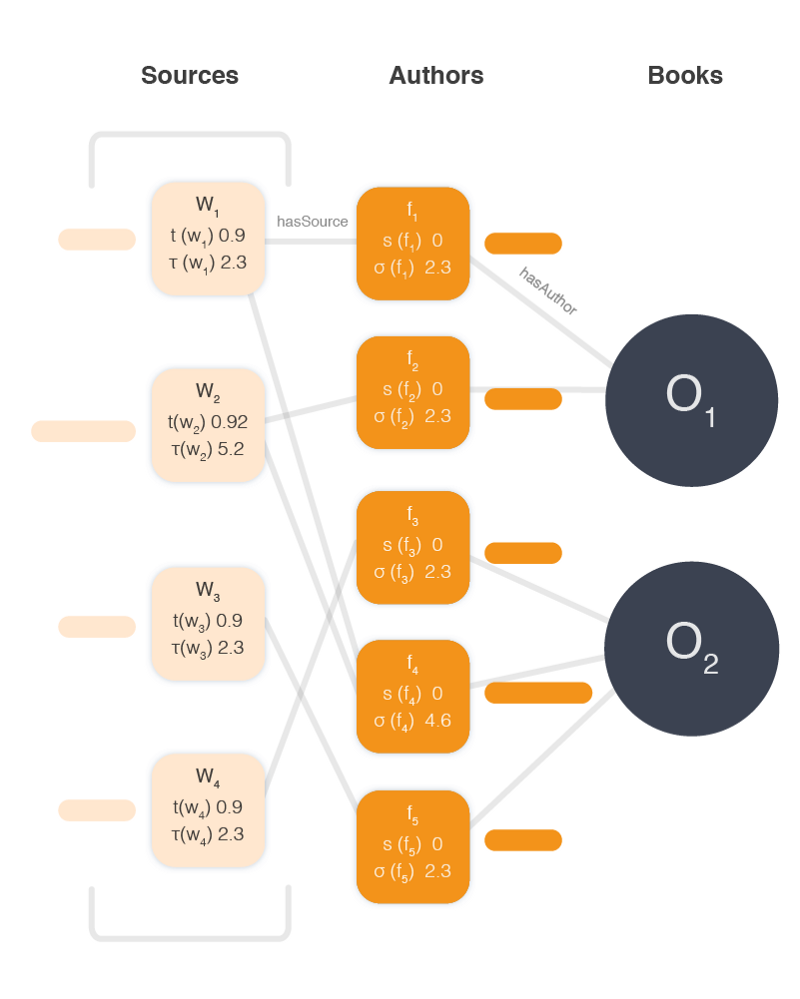
The problem is best represented visually as in the paper, using a graph structure:

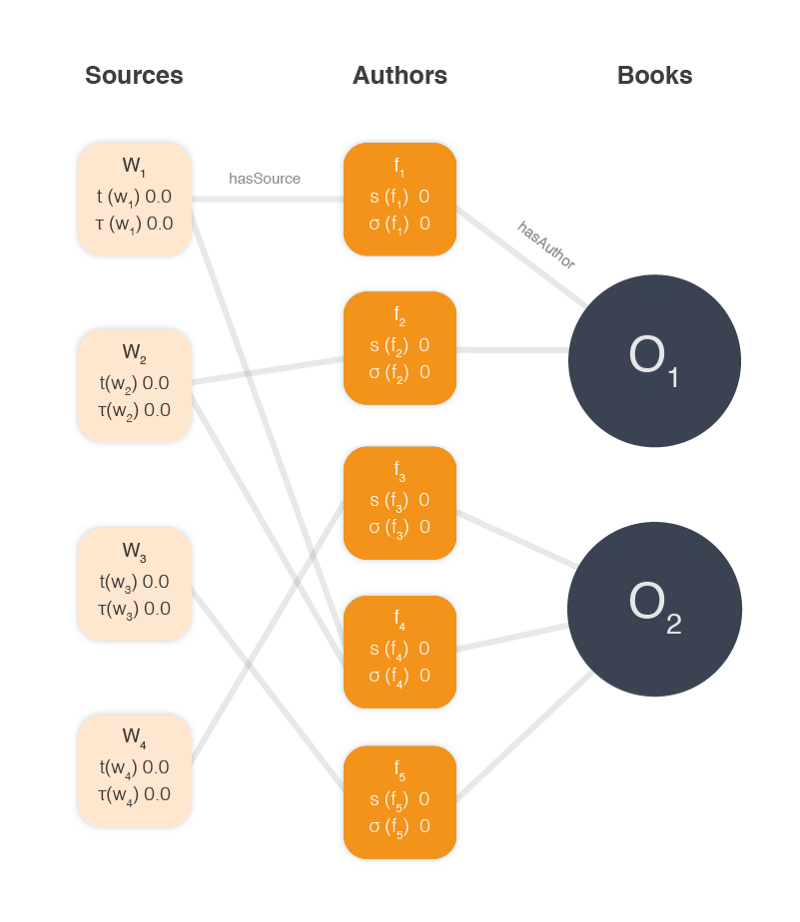
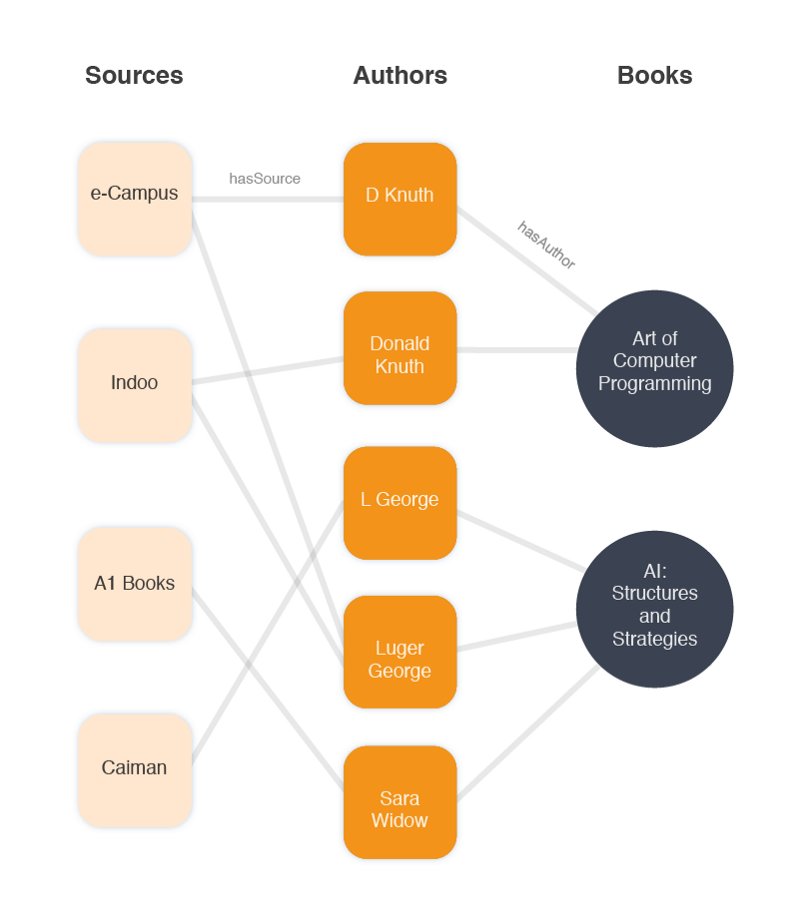
Where w is a source and f is a fact or attribute and o is a book or object. Different sources provide different facts and they provide facts for different objects. All of these facts are of the same type, they all provide authors for books. Here’s our graph with some actual author data filled in.

TruthFinder Algorithm Assumptions

There are some underlying assumptions/heuristics that the TruthFinder algorithm makes use of:

  • There is only one true fact for a property of an object — sometimes referred to as the “single-truth assumption” [3] — a simplification we’ll use.
  • (A) true fact is the same or similar on different web sites — true facts are often similar across sources.
  • False facts on different websites are less likely to be the same or similar — false facts are often more random than true facts.
  • In a certain domain, a web site that provides mostly true facts for many objects will likely provide true facts for other objects — similar to the Authority Hub assumption: a good hub represents a page that points to many other pages, and a good authority represents a page that is linked to by many different hubs.

You may well be thinking these are all very general assumptions and not always true. However, they will serve as a good enough hypothesis for now. Condensed these assumptions become:

  • A fact has high confidence if it is provided by (many) trustworthy websites.
  • A website is trustworthy if it provides many facts with high confidence.

We’ll walk through the 2 major steps in the TruthFinder algorithm [4]:

  1. Compute fact confidence score
  2. Compute source trustworthiness score

Repeat this until there is no change in trustworthiness or fact confidence.

Exploring the Data

Let’s start by exploring the data by loading the data into Pandas and displaying the first 10 rows.

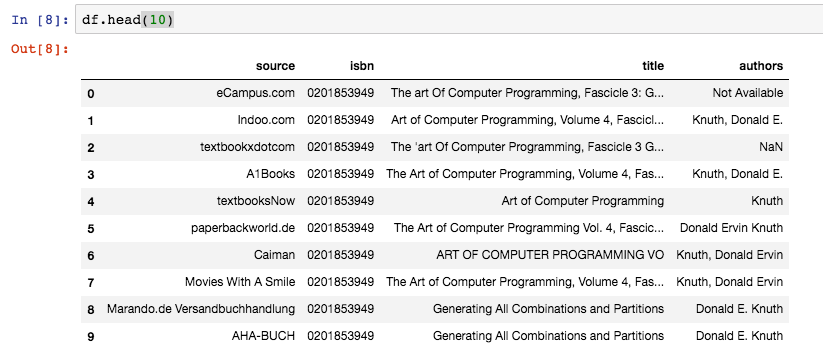
Each book has a unique ISBN identifier, which we’ll use to identify each book also called “object”. Each datapoint has a source, a title and an authors attribute field. The authors field is the fact or attribute that we are trying to reconcile and find the most accurate value for; which author(s) are the correct ones for a specific book.

Additionally checking for row duplicates, with -

sum(data.duplicates())

reveals a substantial number of rows that are identical. Let’s drop all of the duplicates so that our results are not skewed.

data = data.drop_duplicates()

The TruthFinder Steps Explained

Let’s continue defining some constants and initialize our sources to make sure all w (sources) have an equal trustworthiness of 0.9 to start with [1].

max_iteration_count = 10
it = 0
error = 99
tol = 0.001
# intialize source trustworthiness structure
source_trustworthiness = {k: -np.log(1 - 0.9) for k in data['source'].unique()}

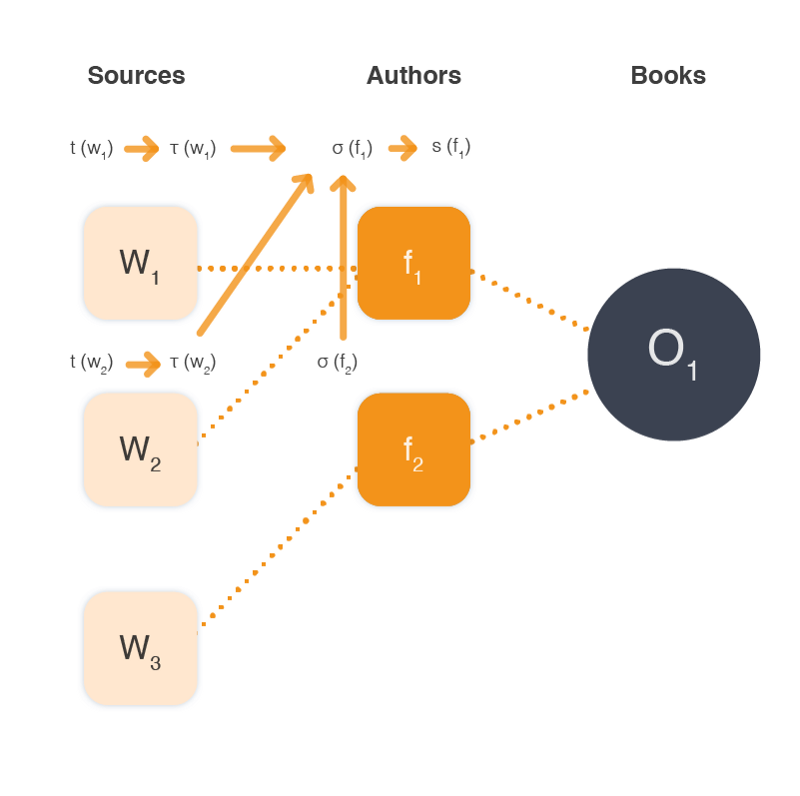
We continue to define the general structure of our iterative process using the basic assumptions/heuristics of the TruthFinder algorithm. Let’s define the iterative process we described so far in Python, defining each step as a separate function for easier implementation.

while error > tol and it < max_iteration_count:
    source_trustworthiness_old = copy.deepcopy(source_trustworthiness)

    # 1. Compute fact confidence score
    data = compute_confidence(data, objects, source_trustworthiness,   attribute_key)

    # 2. Compute source trustworthiness score
    source_trustworthiness = compute_source_trust(data, source_trustworthiness)

    # Check convergence of the process
    error = 1 - np.dot(list(source_trustworthiness.values()),
                       list(source_trustworthiness_old.values()) / (np.linalg.norm(list(source_trustworthiness.values())) *
                                                                    np.linalg.norm(list(source_trustworthiness_old.values()))))

Don’t worry I’ll walk you through each step,

Compute Fact Confidence Score

There are 3 sub-steps to compute the facts confidence using TruthFinder. 

  1. Compute the attribute/facts confidence by summing all source confidence scores from sources providing that exact fact
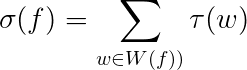
  2. Adjust the confidence score by adding to the score if there are implicating similar facts, but subtract from the score if there are conflicting facts. 
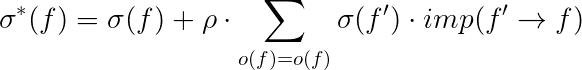
  3. Handle negative probabilities of facts and the independence assumption of sources. Adding a dampening factor gamma to the sigmoid function.

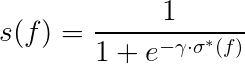
Implementation and detailed explanation of the 3 sub-steps

1. Compute initial fact confidence by summating the log of the trustworthiness of the sources providing that fact.

def compute_confidence(df, objects, source_trust, attribute_key):
    # compute claims confidence score

    all_objects_data = pd.DataFrame()
    for obj in objects:
        data = df[df['object'] == obj]

       # Sub-step 1. compute from source trust
       data, confidence = compute_confidence_score(data, source_trust, attribute_key)

        # Sub-step 2. similarity between claims
        data, confidence = compute_confidence_score_with_similarity(data, confidence, attribute_key)

        # Sub-step 3. compute the adjusted confidence
        data, confidence = compute_final_confidence(data, confidence)

        # concatenate all objects
        all_objects_data = pd.concat([all_objects_data, data])
    return all_objects_data

In this step we want to calculate the fact confidence using the sum of the source trustworthiness for all sources providing that specific fact.

So in our initial instance two sources provide George Luger and the initial state both have 0.9 this would be calculated as follows.

def compute_confidence_score(data, source_trust, attribute_key):
    '''
    compute the confidence score using the sources trust worthiness, sum the scores for all sources
    for a specific claim.
    '''
    # loop through each source for a book
    for idx, claim in data.iterrows():
        # get all sources for a specific claim
        sources = get_sources_for_claim(data, claim, attribute_key)
        # sum the trust score for all the sources for a specific claim
        ln_sum = sum([source_trust[src] for src in sources])
        # set the sum confidence for these facts
        data.at[idx, 'confidence'] = ln_sum

    confidence = data['confidence'].values
    return (data, confidence)

First, we want to get all of the sources that agree on a particular fact. Two sources claims that the author of “Art of computer programming” is “Donald Knuth”. One source claims it is “D. Knuth”. Sum the scores of all sources providing identical facts. Remember at this stage all sources have the same trustworthiness, thus “Donald Knuth” will get double the score of “D. Knuth”.

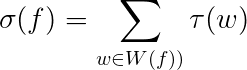
σ(f) is what is called the confidence score, it is the negative log probability of a fact being incorrect by summing τ(w), the confidence scores of all sources w in W(F). τ(w) is the negative log probability of source trustworthiness.

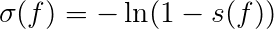
Fact confidence score sigma for confidence s(f)

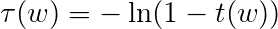
Source trustworthiness score tau for source trustworthiness

Why are these defined like this? Generally computing the fact confidence is defined as follows. 

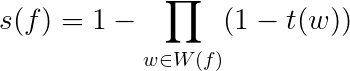
this could lead to underflow in the multiplication (∏ is the symbol for product of a sequence [9]). Another reason is given in the paper “suppose there are two websites w1 and w2 with trustworthiness t(w1) = 0.9 and t(w2) = 0.99. We can see that w2 is much more accurate than w1, but their trustworthiness do not differ much as t(w2) = 1.1 × t(w1). If we measure their accuracy with trustworthiness score, we will find τ (w2) = 2×τ (w1), which better represents the accuracy of websites.”

Given that both sides are logarithms, we can use the logarithmic product rule, to produce the initial equation

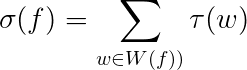
Last thing we do is update the Pandas DataFrame and data sample with this fact confidence score. 

2. Enhance the confidence score for a fact using similarity to other facts

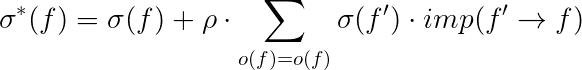
ρ is a number between 0–1 and controls the influence of a fact on another fact. The implication function imp(f’ → f) is a function returning for instance Levenshtein or Jaro Winkler similarity (string distance metrics) between the facts f`and f. I used Jaro-Winkler which tends to work better for names.

sigma_f = 0.9 + 0.9 * ( 0.8*0.9 + 0.6*-0.3)

Facts that are similar are probably implicating other similar facts; George, Luger implicates George Luger F, because the name is identical except for the last initial. This similarity function is domain specific, meaning, it can differ for different attributes. For numerical values, such as country population numbers, the difference between two values might be good enough.

One important property of this implication function is that if the fact is conflicting, we want it to be negative, we solve this by subtracting a base similarity constant. 

def compute_confidence_score_with_similarity(data, confidence, attribute_key):
    '''
    Compute the confidence score of a claim based on its already computed confidence score
    and the similarity between it and the other claims.
    Then set the confidence value to this new confidence computed with similarity measure.
    '''
    # get unique facts for object
    facts_set = data[attribute_key].unique()
    # create fact : confidence dict
    facts_confidence = {x[attribute_key]: x['confidence'] for _, x in data.iterrows()}
    # create an ordered confidence array
    facts_array = np.array(list(facts_confidence.values()))
    # create a copy to assign new adjusted confidence values for
    new_facts_array = copy.deepcopy(facts_array)
    for i, f in enumerate(facts_set):
        # for each source that provides this fact, update its  confidence (similarity factor here, like levenshtein
        similarity_sum = (1 - SIMILARITY_CONSTANT) * facts_array[i] + SIMILARITY_CONSTANT * sum(
            implicates(f, facts_confidence) * facts_array)
        # update the confidence score
        data.loc[data[attribute_key] == f, 'confidence'] = similarity_sum
return (data, new_facts_array)

There is an important caveat mentioned in the paper, if the value of the similarity is less than the base similarity constant (0.5), it will count as a conflicting fact and thus be less than 0 (negative) and for all similarities higher than the base similarity they will be larger than 0 (positive).

import jellyfish
def implicates(fact, fact_sources):
    '''
    How many sources implicates this fact
    :param fact: dataframe row
    :param fact_sources: dataframe
    :return:
    '''
    return [jellyfish.jaro_winkler(fact.lower(),f.lower()) - 0.5 for f in fact_sources]

3. Adjust the facts confidence score

To calculate the fact confidence probability s(f) from σ*(f) we could do

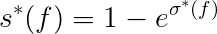
However, this equation assumes that sources are independent, whereas in reality they are not; they copy and steal from each other. To account for this a dampening factor γ is added to the sigmoid function.

Why the sigmoid function? The confidence of a fact f can be negative if f is conflicting with some facts provided by very trustworthy websites. This in turn would make the probability s∗(f) negative. This makes no sense, since even with negative evidences, there is still a real chance that f is correct. To account for this, the paper uses a variety of the widely adopted sigmoid function, but as mentioned adjusted using the gamma dampening factor.

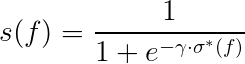
The code below implements the equation above,

def compute_final_confidence(data, confidence):
    for idx, claim in data.iterrows():
        data.at[idx, 'confidence'] = 1 / (1 + np.exp(-DAMPING_FACTOR * claim['confidence']))
    return (data, confidence)

We have now implemented the first part of the algorithm! If you are still with us this far you’ve come a long way. Last stretch ahead.

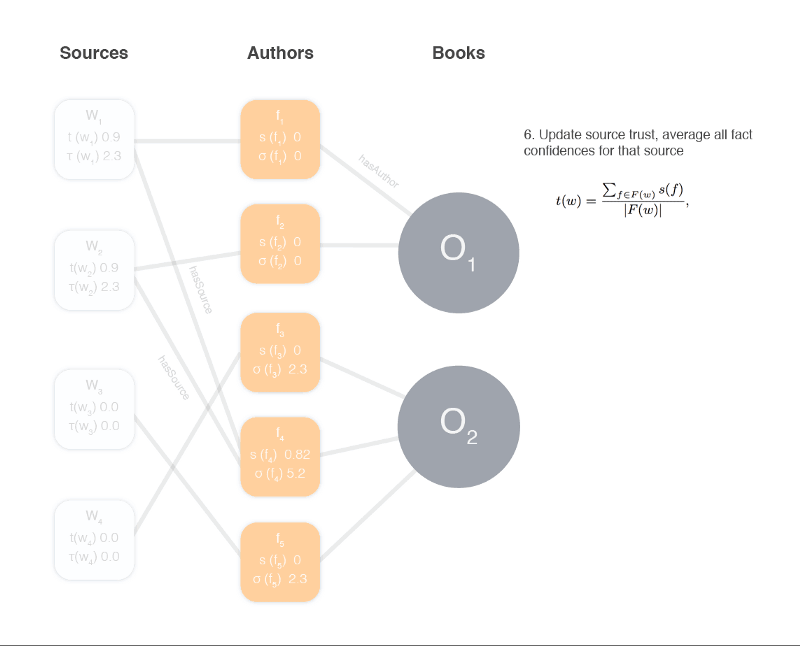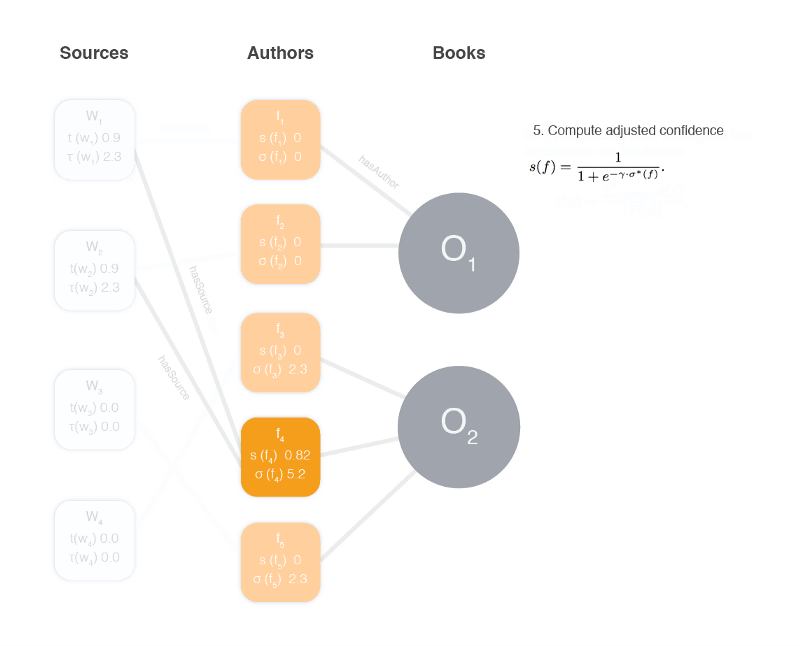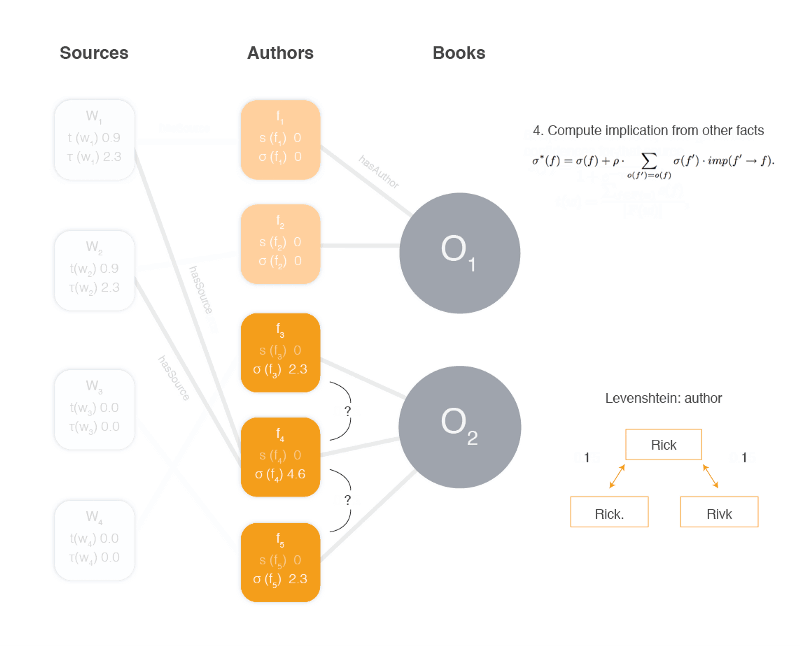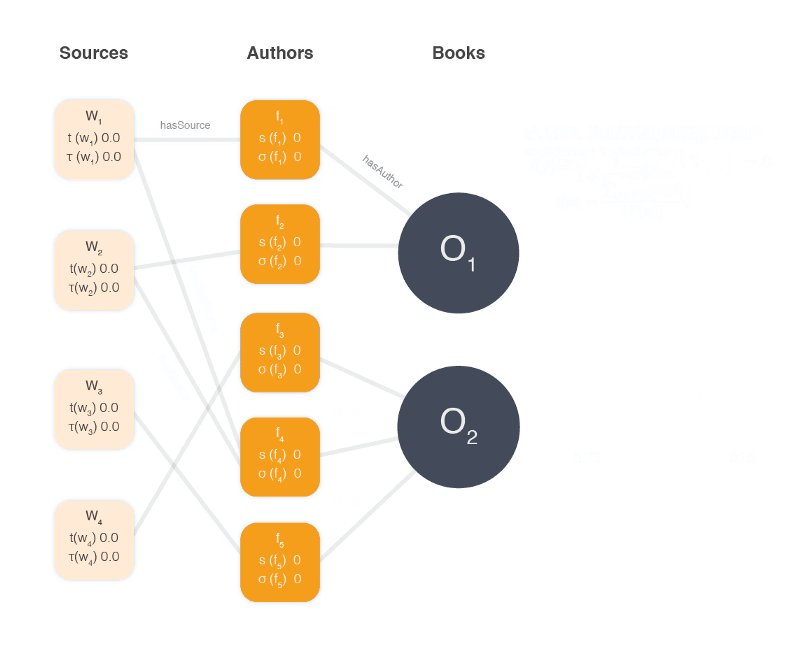
Compute the Source Trustworthiness

This is not as involved as computing the confidence for the facts; source trustworthiness is the average of all the facts from that specific source.

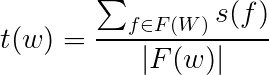
where F(w) is the set of facts provided by w [1].

def compute_source_trust(data, sources):
    '''
    Compute every source trustworthiness. The trustworthiness score is the average confidence of
    all facts supplied by source w
    :param data: Dataframe all facts for object O
    :param sources: dict all unique sources and current scores
    :return: dict of unique sources with updated scores
    '''
    for source in sources:
            # t(w) trustworthiness of website w
            # the average confidence of all facts supplied by website/source w
            t_w = sum([confidence for confidence in data[data['source'] == source]['confidence'].values]) / len(
                data[data['source'] == source].index)
            # tau(w) trustworthiness score of website w
            # as explained in the paper, 1 - t(w) is usually quite small and multiplying many of them
            # might lead to underflow. Therefore we take the logarithm of it to better model how trustworthy a source is
            tau_w = -np.log(1 - t_w)
            # update the source score to the new score
            sources[source] = tau_w
    return sources

We loop through each source and retrieve all confidence values from all facts that source provides about different objects. We get the average of these confidence score, to get the average confidence score for the facts provided by that source.

Finally if we want the probability s(f) we do ln(1 — confidence score) of the source.

Final Steps

That is it! Now if we continuously iterate and update the facts confidence and consecutively the source trust score, we will eventually reach an equilibrium where the scores won’t change. 

error = 1 - np.dot(list(source_trustworthiness.values()), list(source_trustworthiness_old.values()) / (
        np.linalg.norm(list(source_trustworthiness.values())) * np.linalg.norm(
    list(source_trustworthiness_old.values()))))

The result will be a list of our source trustworthiness scores and a score for each fact. We select the fact for each object that has the highest confidence score. 

Results and Conclusion

The golden set of authors can be found here. Comparing the results of the paper with my implementation is unfortunately very difficult, because of the author cleaning and accuracy scoring differs greatly from the original paper. 

However this implementation of TruthFinder gave a 10% relative improvement compared to simple naive majority voting.

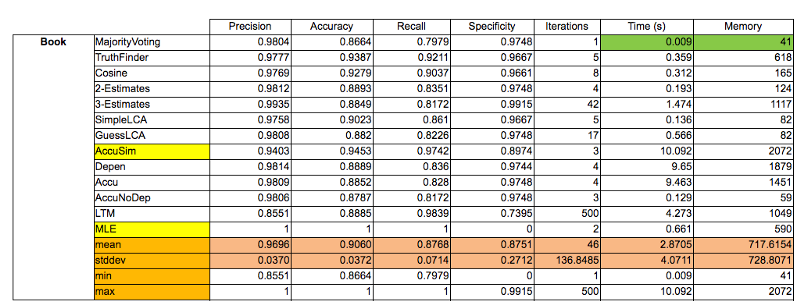
This post is an attempt to serve as an introduction to data fusion of multiple conflicting sources. If you arrived all the way down here, you might already be thinking of both simpler and more sophisticated methods [5] to solve this problem. A simpler one, is a naive majority voting, counting which fact is provided by the most sources. However, simple majority voting can be problematic, as sources might be biased and plagiarism between sources is common [8].

There are a plethora of methods that are more sophisticated, more accurate and supports more use-cases. Some interesting papers are referenced in the References section for further exploration.

Hopefully this post enables and encourages you to create your initial data fusion prototype for whatever use case you may have. Let me know if you create something cool or if you have any feedback on the post.

I work in the Knowledge Graph team at Meltwater where we do this stuff all day. You can learn more about what we do at fairhair.ai, underthehood.meltwater.com, and meltwater.com.

Acknowledgments

Thanks also to all, mostly colleagues, that provided valuable feedback on the post. Thanks to Norah Klintberg Sakal, for additional feedback.

All equations created with eqneditor.

References

This post was originally published at medium.com/fairhairai/data-integration-in-practice-fusing-conflicting-datasources-5ea470ac66e2.