Locality-sensitive Hashing in Elixir

My team and I have built a solution that mines a stream of online articles for real-time insights for our customers. This component’s logic could be dramatically simplified if we could assume that it never receives near-duplicates of articles. While deduplication of identical documents is simple, detection of near-duplicates (i.e. “same thing, just slightly different”) is a complex but well-researched problem space.

To solve our problem, we ended up building a locality-sensitive hashing library for Elixir. Read on to find out why and how we built and open-sourced ExLSH.

Our Challenge in more Detail

One of our components mines a stream of news articles from online publications. The solution works better if it only processes a story once - and not every time when it gets reprinted by several outlets. The component is built using Elixir, a functional language built on top of the battle-tested Erlang ecosystem. Hence we needed a near-duplicate detection solution that works well with Elixir.

The usual solution used in the industry is called locality-sensitive hashing (LSH). This technique is also known as similarity hashing, Charikar hash, similarity hash, or sim-hash. We have reviewed what LSH libraries are available for Elixir. The one we have found is called SimHash and it targets another use-case (1-on-1 comparisons of short strings like usernames, URLs, etc.). We anticipated running a lot of experiments to fine-tune the deduplication rate, so we needed configurability that was not provided by SimHash. Another library called SpiritFingers has similar configurability limitations but a faster implementation than SimHash.

During an internal Hackathon we built our own LSH implementation in Elixir, which we dubbed ExLSH. We open sourced this library at github.com/meltwater/ex_lsh and if the only thing you need is a fast locality-sensitive hashing for Elixir, then this might be a good choice for you.

Read on if you want to learn more about the hashing algorithm and really care about how we made this faster :)

LSH in a Nutshell

A hash function maps a large input space (in our case, all online news articles) to a very small output space (usually a fixed-length sequence of bits). Hash functions are usually referred to as “one-way”: it’s easy to compute the output but not possible to reconstruct the input from a hash. Due to this property, hash functions are mostly employed in cryptography. Most well-known hash functions are optimized for generation of very different outputs even for very similar inputs, producing as few collisions as possible. A collision occurs when two non-identical inputs result in the same hash output. In contrary to cryptographic hashes, a locality-sensitive hash produces very similar outputs for very similar documents, and optimizes for more collisions. If the output space is small enough, an LSH regularly generates collisions on similar documents. Then we can remove near-duplicates from a stream using a simple lookup in a sliding window. More advanced techniques exist.

A common algorithm to compute a locality-sensitive hash is called SimHash. This article by Moz describes it in detail. Here, we will focus on how we implemented it:

First, the input text is normalized: this involves unicode normalization, downcasing and removal of punctuation
Normalized input is tokenized, i.e. split into words or characters
Tokens are combined into shingles, or n-grams, to retain the order of their appearance in the input. If you don’t care about the order, skip this step by setting shingle width to 1.
Tokens are filtered by a user-provided function. Use this if you have a stoplist, e.g for articles and other common words.
Every shingle is hashed using a hash function, e.g. MD5. Recap: small change in the input yields big change in the hash!
Hashes are converted from bit to vector representation, where every set bit becomes a +1, and every zero bit becomes a -1
All shingle hash vectors are added into one vector of integers
The sum vector is converted into bits, with all negative positions set to 0, and all others set to 1. The width of the vector is the same as that of the hash function, hence the collision probability gets higher with smaller hashes: high for MD5, low for SHA-512.

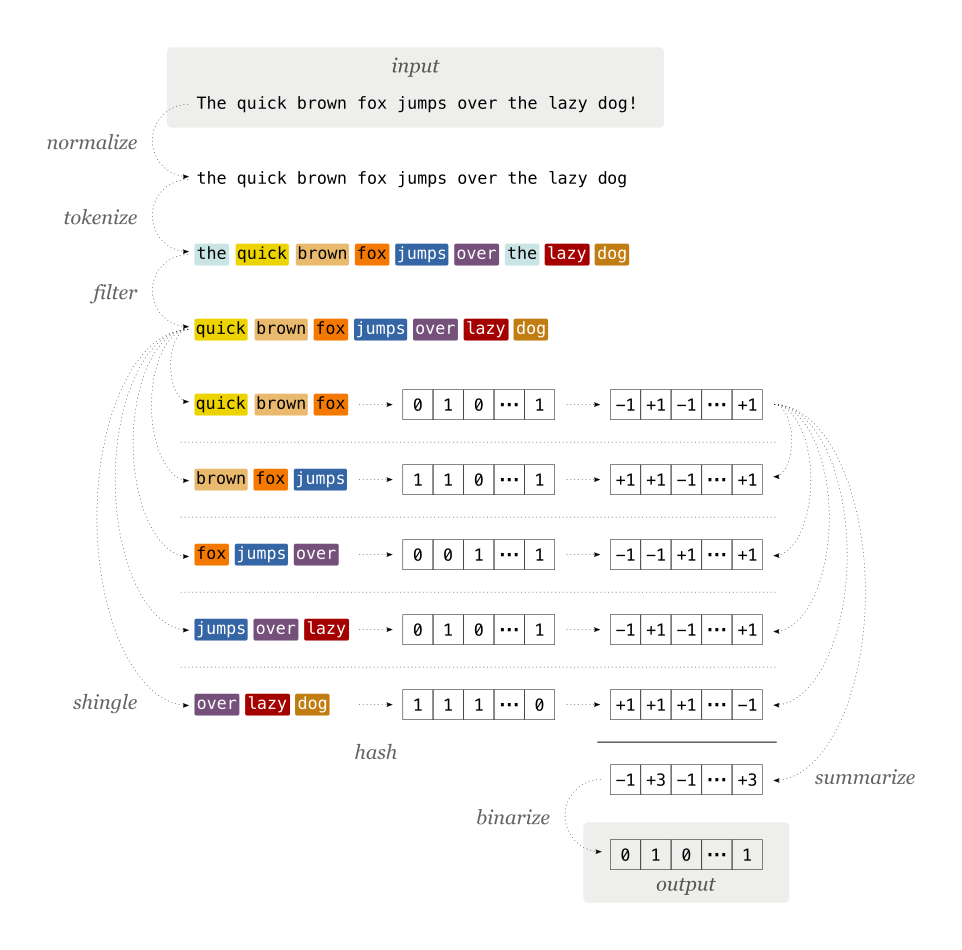
ExLSH algorithm overview

Figure 1: Step-by-step visualization of the locality-sensitive hash algorithm.

Configurability

The key feature of ExLSH is its configurability. Every deduplication use-case will have its own set of requirements for hash size, collision probability, etc. ExLSH allows you to define how the input is preprocessed (normalization, tokenization, filtering, shingling) and which hash algorithm is used:

# 4-grams and MD5
iex(1)> "lorem ipsum dolor sit" |> ExLSH.lsh(4, &:crypto.hash(:md5, &1)) |> Base.encode64()
"X2Vs9ee9Uk38p6pkUIhlZQ=="

# no shingling ("bag-of-words") and SHA-256
iex(2)> "lorem ipsum dolor sit" |> ExLSH.lsh(1, &:crypto.hash(:sha256, &1)) |> Base.encode64()
"BABBQURRDEiogqAAISKIKAWAQEQZAAgrUtTgXD5FDaA="

We also provide two handy helper functions that run a pre-configured LSH for a long or a short text.

# use this for documents
iex(1)> "lorem ipsum dolor sit" |> ExLSH.wordwise_lsh() |> Base.encode64()
"OEAhAhKSgBAwgQEAgCCAEg=="

# use this for short strings (usernames, URLs, slugs)
iex(2)> "username" |> ExLSH.charwise_lsh() |> Base.encode64()
"FPIBaaBQGlKKARlqA9lb1g=="

Making ExLSH Faster

After using the library in production, we discovered that the near-duplicate detection puts a significant load on the CPU. To understand where the ExLSH.lsh/1 function spends most of its cycles, we have used one of the Erlang profiling tools, fprof. Elixir’s build tool mix provides a command to run fprof, so all we had to do is write a script bench.exs:

text = "lorem ipsum dolor sit"
ExLSH.lsh(text)

and profile it with mix profile.fprof bench.exs, yielding this result:

ExLSH algorithm overview

The results are comparable to a flamegraph. The functions are sorted by how much time they cost including all other functions they call (ACC column). The interesting part is the OWN column that shows how much time the functions spent running its own body (not calling out to others). There is a hotspot in ExLSH.sum_binaries/2 - it ran 6766 times, spending 14.8 ms on its own instructions. Let’s have a look at what it does:

def sum_binaries(
    <<b0::size(1), b1::size(1), b2::size(1), b3::size(1), b4::size(1), b5::size(1),
        b6::size(1), b7::size(1), bin_rest::bitstring>>,
    [agg0, agg1, agg2, agg3, agg4, agg5, agg6, agg7 | agg_rest]
    ) do
[
    agg0 + b0 * 2 - 1,
    agg1 + b1 * 2 - 1,
    agg2 + b2 * 2 - 1,
    agg3 + b3 * 2 - 1,
    agg4 + b4 * 2 - 1,
    agg5 + b5 * 2 - 1,
    agg6 + b6 * 2 - 1,
    agg7 + b7 * 2 - 1
    | sum_binaries(bin_rest, agg_rest)
]
end

def sum_binaries(<<>>, []), do: []

This function receives a binary representation of a shingle’s hash, and a list of integers for the bitwise aggregation (see Figure 1 above). The function parses the leftmost byte of the hash into individual bits using binary pattern-matching, and deconstructs the first eight bit-counters in a very similar way. It adds 1 for every set bit, while subtracting 1 for every unset bit and delegates the rest of the bytes in the hash/accumulator to itself via tail recursion.

The cost of recursion in Erlang/Elixir is lower than in non-functional languages such as Java, but considering the pattern-matching involved, it is not zero. So we experimented with parsing 16 bits at a time, which gave us slightly faster results. This indicated that if we pattern match on more bits per recursion we would gain performance. However, writing out pattern matching manually for even 16 bits was very cumbersome and barely readable:

def sum_binaries(
    <<b0::size(1), b1::size(1), b2::size(1), b3::size(1), b4::size(1), b5::size(1),
        b6::size(1), b7::size(1), b8::size(1), b9::size(1), bA::size(1), bB::size(1),
        bC::size(1), bD::size(1), bE::size(1), bF::size(1), bin_rest::bitstring>>,
    [
        agg0,
        agg1,
        agg2,
        agg3,
        agg4,
        agg5,
        agg6,
        agg7,
        agg8,
        agg9,
        aggA,
        aggB,
        aggC,
        aggD,
        aggE,
        aggF | agg_rest
    ]
    ) do
[
    agg0 + b0 * 2 - 1,
    agg1 + b1 * 2 - 1,
    agg2 + b2 * 2 - 1,
    agg3 + b3 * 2 - 1,
    agg4 + b4 * 2 - 1,
    agg5 + b5 * 2 - 1,
    agg6 + b6 * 2 - 1,
    agg7 + b7 * 2 - 1,
    agg8 + b8 * 2 - 1,
    agg9 + b9 * 2 - 1,
    aggA + bA * 2 - 1,
    aggB + bB * 2 - 1,
    aggC + bC * 2 - 1,
    aggD + bD * 2 - 1,
    aggE + bE * 2 - 1,
    aggF + bF * 2 - 1
    | sum_binaries(bin_rest, agg_rest)
]
end

So we decided to generate the cases for 8, 32, 64, 128 and even 256 bits programmatically using a macro. Designing that macro was untrivial and we’re still learning; see the source here. This is how we call the macro from the main module:

for i <- [256, 128, 64, 32, 8] do
  ExLSH.BitMacro.vector_reducer(i)
end

Elixir will test the pattern matching in function clauses in the order in which they appear in the module. We start with the widest to leverage the wider matchers. With this optimization, SHA-256 will need only one invocation of the first clause per shingle, instead of 32 in the original version! MD5 will match on the second clause, and RIPEMD-160 will use 256, then 64, then 32 - resulting in 3 calls total per shingle - instead of 20! In a realistic benchmark, this brought down the number of recursions from 6766 to 796 on the same dataset, and resulted in a speedup of x1.89 (47% less time spent computing an LSH). We have benchmarked ExLSH against SimHash, and the former is faster by approximately factor 7!

In Closing

In the meanwhile, we have deployed the updated faster ExLSH in production and run the service in Kubernetes using autoscaling on CPU. This works out pretty well for us so far!

ExLSH is available on hex.pm, and its docs are hosted on hexdocs.pm. If you are looking to solve a deduplication problem similar to ours, give ExLSH a try! If you have questions, or feature requests feel free to reach out and file an issue over at GitHub!